Mickaël Ly

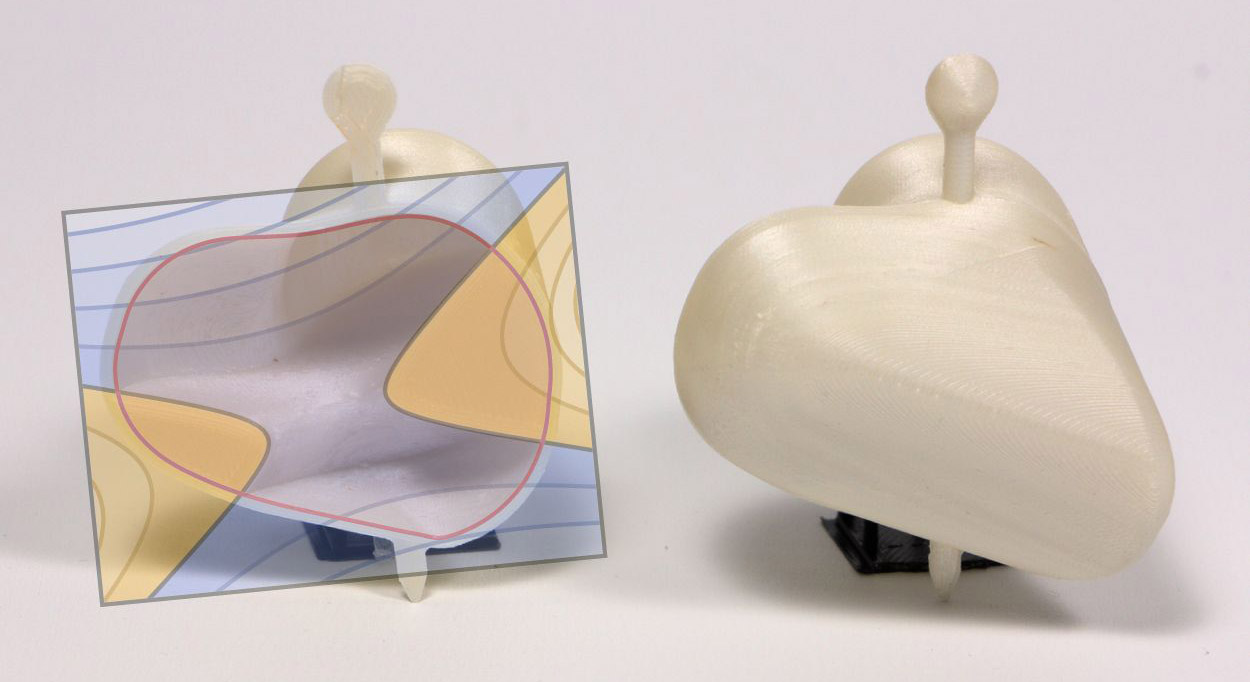
Spin-It Faster: Quadrics Solve All Topology Optimization Problems That Depend Only On Mass Moments
(website, paper, supplemental, video)
Christian Hafner, Mickaël Ly, Chris Wojtan
ACM Transactions on Graphics (Siggraph 2024)
Honorable Mention from the Siggraph 2024 Technical Papers Awards
Abstract ⤵ The behavior of a rigid body primarily depends on its mass moments, which consist of the mass, center of mass, and moments of inertia. It is possible to manipulate these quantities without altering the geometric appearance of an object by introducing cavities in its interior. Algorithms that find cavities of suitable shapes and sizes have enabled the computational design of spinning tops, yo-yos, wheels, buoys, and statically balanced objects. Previous work is based, for example, on topology optimization on voxel grids, which introduces a large number of optimization variables and box constraints, or offset surface computation, which cannot guarantee that solutions to a feasible problem will always be found. In this work, we provide a mathematical analysis of constrained topology optimization problems that depend only on mass moments. This class of problems covers, among others, all applications mentioned above. Our main result is to show that no matter the outer shape of the rigid body to be optimized or the optimization objective and constraints considered, the optimal solution always features a quadric-shaped interface between material and cavities. This proves that optimal interfaces are always ellipsoids, hyperboloids, paraboloids, or one of a few degenerate cases, such as planes. This insight lets us replace a difficult topology optimization problem with a provably equivalent non-linear equation system in a small number (<10) of variables, which represent the coefficients of the quadric. This system can be solved in a few seconds for most examples, provides insights into the geometric structure of many specific applications, and lets us describe their solution properties. Finally, our method integrates seamlessly into modern fabrication workflows because our solutions are analytical surfaces that are native to the CAD domain.

Primal–Dual Non-Smooth Friction for Rigid Body Animation
(website, paper, supplemental, video, additional video,)
Yi-Lu Chen, Mickaël Ly, Chris Wojtan
ACM Siggraph 2024 Conference Papers
Abstract ⤵ Current numerical algorithms for simulating friction fall in one of two camps: smooth solvers sacrifice the stable treatment of static friction in exchange for fast convergence, and non-smooth solvers accurately compute friction at convergence rates that are often prohibitive for large graphics applications. We introduce a novel bridge between these two ideas that computes static and dynamic friction stably and efficiently. Our key idea is to convert the highly constrained non-smooth problem into an unconstrained smooth problem using logarithmic barriers that converges to the exact solution as accuracy increases. We phrase the problem as an interior point primal-dual problem that can be solved efficiently with Newton iteration. We observe quadratic convergence despite the non-smooth nature of the original problem, and our method is well-suited for large systems of tightly packed objects with many contact points. We demonstrate the efficacy of our method with stable piles of grains and stacks of objects, complex granular flows, and robust interlocking assemblies of rigid bodies.

Unified treatment of contact, friction and shock-propagation in rigid body animation
(website)
Yi-Lu Chen, Mickaël Ly, Chris Wojtan
Proceedings of the Symposium on Computer Animation 23 (SCA)
Abstract ⤵ We present a rigid body animation technique which prevents solids from interpenetrating, dissipates energy through friction, and propagates shocks through contacts. We employ the Alternating Direction Method of Multipliers (ADMM) to couple non-smooth Coulomb friction with impact propagation, allowing efficient and accurate non-smooth dynamics along with a correct transmission of impacts through assemblies of rigid bodies. We further extend our method to model adhesion, dynamic friction and lubricated contact.

Static inverse modelling of clothes
(website, manuscript)
Mickaël Ly - PhD Thesis, 2021
Honorable mention for the AFIG's (Eurographics French Chapter) PhD Award 2022

Physical validation of simulators in Computer Graphics: A new framework dedicated to slender elastic structures and frictional contact
(website, paper, accompanying video, supplemental , recipe manual for the tests )
Victor Romero, Mickaël Ly, Abdullah-Haroon Rasheed, Raphaël Charrondière, Arnaud Lazarus, Sébastien Neukirch, Florence Bertails-Descoubes
ACM Transactions on Graphics 2021 (SIGGRAPH)
Abstract ⤵ We introduce a selected set of protocols inspired from the Soft Matter Physics community in order to validate Computer Graphics simulators of slender elastic structures possibly subject to dry frictional contact. Although these simulators were primarily intended for feature film animation and visual effects, they are more and more used as virtual design tools for predicting the shape and deformation of real objects; hence the need for a careful, quantitative validation. Our tests, experimentally verified, are designed to evaluate carefully the predictability of these simulators on various aspects, such as bending elasticity, bend-twist coupling, and frictional contact. We have passed a number of popular codes of Computer Graphics through our benchmarks by defining a rigorous, consistent, and as fair as possible methodology. Our results show that while some popular simulators for plates/shells and frictional contact fail even on the simplest scenarios, more recent ones, as well as well-known codes for rods, generally perform well and sometimes even better than some reference commercial tools of Mechanical Engineering. To make our validation protocols easily applicable to any simulator, we provide an extensive description of our methodology, and we shall distribute all the necessary model data to be compared against.

Projective Dynamics with Dry Frictional Contact
(website, paper, accompanying video, code )
Mickaël Ly, Jean Jouve, Laurence Boissieux, Florence Bertails-Descoubes
ACM Transactions on Graphics 2020 (SIGGRAPH)
Abstract ⤵ Projective dynamics was introduced a few years ago as a fast method to yield an approximate yet stable solution to the dynamics of nodal systems subject to stiff internal forces. Previous attempts to include contact forces in that framework considered adding a quadratic penalty energy to the global system, which however broke the simple, constant matrix, structure of the global linear equation, while failing to treat contact in an implicit manner. In this paper we propose a simple yet effective method to integrate in a unified and semi-implicit way contact as well as dry frictional forces into the nested architecture of Projective dynamics. Assuming that contacts apply to nodes only, the key is to split the global matrix into a diagonal and a positive matrix, and use this splitting in the local step so as to make a good prediction of frictional contact forces at next iteration. Each frictional contact force is refined independently in the local step, while the original efficient structure of the global step is left unchanged. We apply our algorithm to cloth simulation and show that contact and dry friction can be captured at a reasonable precision within a few iterations only, hence one order of magnitude faster compared to global implicit contact solvers of the literature.

Inverse Elastic Shell Design with Contact and Friction
(website, paper, accompanying video, press release)
Mickaël Ly, Romain Casati, Florence Bertails-Descoubes, Mélina Skouras, Laurence Boissieux
ACM Transactions on Graphics 2018 (SIGGRAPH Asia)
Abstract ⤵ We propose an inverse strategy for modeling thin elastic shells physically, just from the observation of their geometry. Our algorithm takes as input an arbitrary target mesh, and interprets this configuration automatically as a stable equilibrium of a shell simulator under gravity and frictional contact constraints with a given external object. Unknowns are the natural shape of the shell (i.e., its shape without external forces) and the frictional contact forces at play, while the material properties (mass density, stiffness, friction coefficients) can be freely chosen by the user. Such an inverse problem formulates as an ill-posed nonlinear system subject to conical constraints. To select and compute a plausible solution, our inverse solver proceeds in two steps. In a first step, contacts are reduced to frictionless bilateral constraints and a natural shape is retrieved using the adjoint method. The second step uses this result as an initial guess and adjusts each bilateral force so that it projects onto the admissible Coulomb friction cone, while preserving global equilibrium. To better guide minimization towards the target, these two steps are applied iteratively using a degressive regularization of the shell energy. We validate our approach on simulated examples with reference material parameters, and show that our method still converges well for material parameters lying within a reasonable range around the reference, and even in the case of arbitrary meshes that are not issued from a simulation. We finally demonstrate practical inversion results on complex shell geometries freely modeled by an artist or automatically captured from real objects, such as posed garments or soft accessories.